探究/ケーススタディ(1)...四角中点/モンスターとその排除
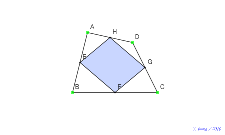
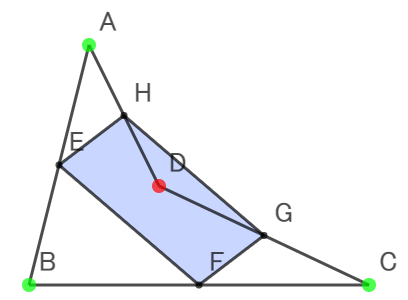
- 四角形ABCDの4つの辺AB,BC,CD,DAのそれぞれの中点をE,F,G,Hとする。図を動かしたとき,どんなことに気づきますか?
「モンスター」とその排除
観察されうる「モンスター」
- 上記の対応表をつくるとき,「四角形の種類」を念頭において形をつくることが想定されているが,4つの点を自由に動かす環境なので,それらをあまり考えずに,次のような場合をつくることもありうる。
- あるいは,「EFGHはいつも平行四辺形」という命題が意識化されると,「そうならない場合は本当にないのだろうか」という意識で下記を生成することもありうる。
モンスターへの対処
- この形は,中学校でも,「場合によっては四角形」として扱っている。
- 逆にいえば,暗黙のうちに凸四角形のみを四角形として扱っている場合もある。
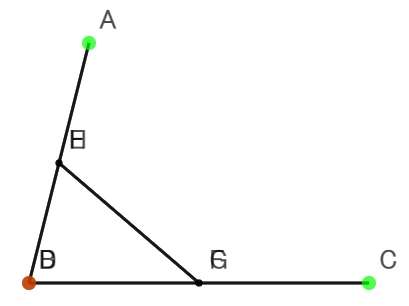
- この形(たとえば,くさび形というような名称をつけるとすると)を,四角形として扱うのが適切かどうかを検討することが,ここで必要なことになる。
- これは,いわば四角形としては「退化している」場合といってもいい。
- さらに,1つの点に4つを重ねるようなケースもある。
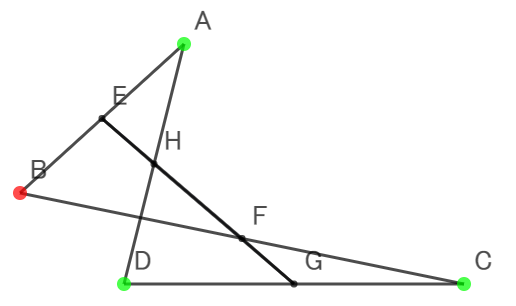
- 「平行四辺形にならない」場合の発見といっても,本質的な反例として受け止めるほどではないとなるだろう。
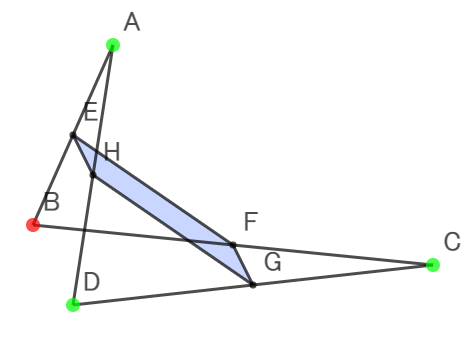
- 「平行四辺形にならない」場合としては,こちらの方が重みがある。
- 退化する特殊な場合だけでなく,ある条件を満たす場合はいつもそうなることが推定される。
- 中点連結定理との関わりで,それを説明することも意味がある。
- 一方,これは四角形として扱うべきかどうかについては,きっと議論が分かれて,「扱う必要性は感じない」のかもしれない。
- 上記との関わりでいえばABCDは四角形として扱うのが適切とは思えないように感じるが,EFGHは平行四辺形,つまり命題としての結論が成り立ってるという点で,「きちんと扱うべき」ことが示唆される事実といえる。
- まわりに線分を追加して,「辺の中点と対角線の中点を結んだら」と,命題の記述を変える
- まわりに線分を追加して,3次元と解釈し,四面体の4つの辺の中点を結ぶと,命題の記述を変える。
ABCDとEFGHの面積の関係に注目する
ABCDは,4つの三角形と一つの四角形に分割されていると考え,4つの三角形の関係に注目する
点Aだけを動かして,「EFGHがどういう形になるか」に注目する
二つの点の動かし方と,「EFGHの形」との関わりに注目する
四つの点の動かし方と,「EFGHの形」との関わりに注目する